特徴化技術
田口玄一博士が1995年にMT法(MTS)を提案したとき、文字や波形パターンの特徴化のアイディアも併せて提案しました。特徴化のアイディアとは、パターンに複数の線を定義し、線がパターンを横切る数や線上のパターンの量を数えるという方法です。そしてマハラノビス距離とのセットを、マハラノビス・タグチ・システム(MTS)と命名しました。セットとしての定義はあまり知られていませんが、当時の品質工学会誌に記載されています。
田口博士はこれらの特徴量を「微分特性」「積分特性」と名付けました。しかし意味が分かりにくいため、後年私たちは「変化量」「存在量」と呼ぶことにしました。意味は以下のとおりです。

文字パターンの場合:
左図は数字5を横5×縦7のグリッドに書いたパターンです。中央の4行目に赤い線を描いてありますが、この線上のパターンが白→黒あるいは黒→白と変化する数を数えます。この場合は2回変化していますので、“変化量=2”となります。また、赤線の上の黒いグリッド数は4個ありますので、“存在量=4”となります。これを上から下まで数えると、変化量は(1,2,2,2,1,1,1)となり、存在量は(5,1,1,4,1,1,5)となります。全部で14個の特徴量となります。
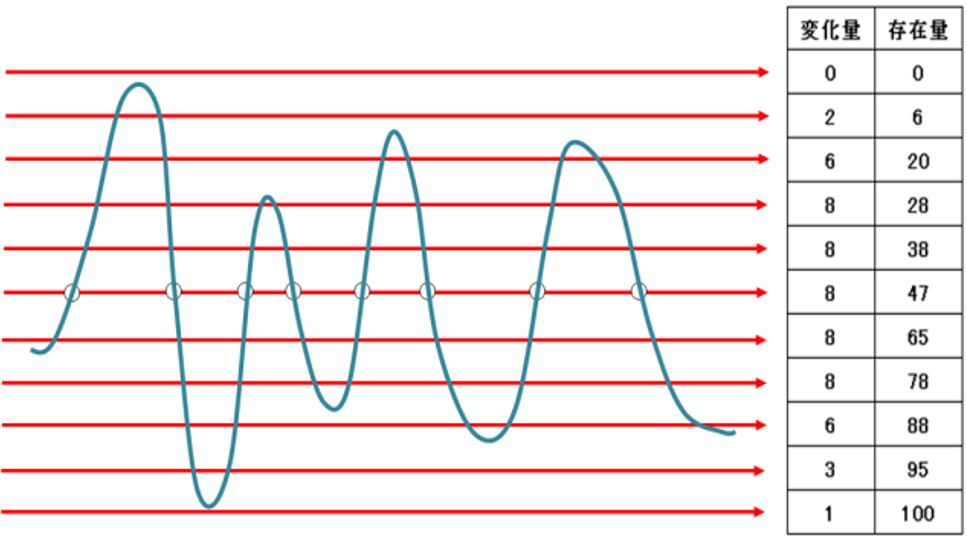
波形パターンの場合(1):
考え方は文字パターンの場合と同じですが、変化量・存在量を求めるために複数の横線を設定します。この線を「標本線」と呼びます。左図では11本の線が引かれており、各線から変化量・存在量が抽出されますので、合計22個の特徴量となります。標本線の上下位置や本数は正常波形を技術者の目で見て、適切に設定します。ポイントをつかめばそれほど難しい作業ではありません。
振動波形では数千~数万サンプルありますから、数百サンプルずつに分けて特徴抽出するのが一般的です。
振動や音などの特徴量としては、周波数解析(FFT)などが利用されてきましたが、ここに示した方法を適用すると、より高感度な異常検知が可能です。
波形パターンの場合(2):「波の形」の特徴化
電流波形の形、圧力波形の形あるいはスペクトル波形など、山の形が正常か否かを評価する必要に迫られることがあります。
図ではたくさんの山形状がありますが、それぞれが同じかどうか数値で知りたいでしょう。
MTシステム(MT法)では、山の形を適切に特徴化する技術が提供されています。
深層学習より優れた結果を得ることができます。
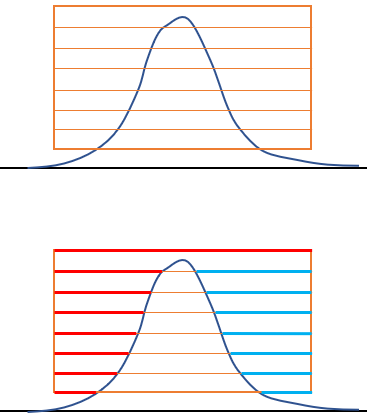
ものづくりにおける「山の形」の特徴化技術(アングルトライの特許技術)
少しずつ形が異なる3つの山があるとします。

MTシステムでは以下のように特徴化します。
まず、山全体を囲む四角形の領域を定義します。
そこに複数の横線(標本線)を引きます。
山の形の特徴化
各標本線について、四角形の左端から山にぶつかるまでの長さ(開始長)を求めます。赤い線です。そして、四角形の右端から逆方向に山にぶつかるまでの長さ(終了長)を求めます。青い線です。

赤い線と青い線だけを抜き出すと、図のようになります。
図の左右に、長さも表示しています。
MT法でこの特徴量を扱う場合には、下のように横並びになります。

この数値組み合わせが、波形形状を意味します。3つの山から特徴量だけを取り出した図を下に示します。

標本線数が多いほど精密な形状情報にはなりますが、多くの課題では、それほど密にしなくても目的を達成することができます。
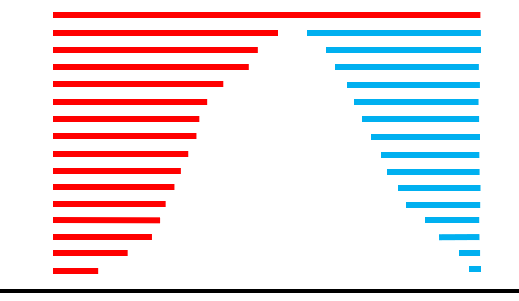
この特徴化技術は、電流波形やスペクトル波形に応用することができ、多くの課題では深層学習より優れた結果を得ることが確認されています。
そのほか、画像検査でも大きな威力を発揮します。
画像データは膨大な輝度波形、すなわちスペクトルの集合だからです。
そして、ATSpectrum や REM-Image で利用することができます。
なお、ここでご説明した技術は数件の特許となっています。
