T法（１）・MSR

T法(1)

T法(1)は、重回帰分析と同様「出力値の推定を行う数理」です。複数の項目、すなわち説明変数から出力値を推定します。
T法(1)では、各項目と出力値の関係をそれぞれ求めてから総合します。総合するに当たっては、項目間の相関は考慮しません。一定の割り切りで利用できる方法です。
また、“項目数≧サンプル数”でも計算できることも大きな利点です。
下の図は、25項目×12サンプルのデータによる実績値（横軸）と推定値（縦軸）との散布図です。この事例は重回帰分析では計算が不可能です。

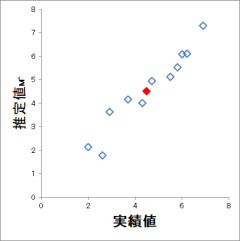
膜厚形成に関する実績値（横軸）と推定値の関係

T法（１）では、「項目ごとの推定値への寄与度」を分析することができます。下の図では、項目5が推定値を上げることに寄与することなどが分かります。

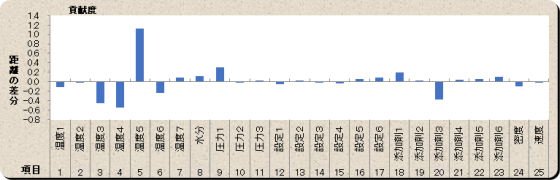
T法（１）の診断結果

MSR （Multiple Single Regression）

MSRは、T法(1)の改良を目的に開発された推定の手段です。深層学習と同様に、繰り返し計算により誤差を最小化する数理を用いており、以下の特徴があります。
(1) 相関の要素が推定式に織り込まれ、その程度は重回帰分析ほど過度にならない
(2) ほとんどのケースで、T法(1)や重回帰分析より精度のよい安定した推定ができる
(3) サンプル数が項目数より少ない場合でも、精度のよい推定式が得られる

MSRでも「項目ごとの推定値への寄与度」を分析することができます。
MSRの数理の詳細は以下論文をご参照ください。
前田誠 : T法（１）の考え方を利用した新しい回帰法の提案，品質, 47、[2] (2017),p.71-80, 日本品質管理学会