MTシステム問答・応用編⑥
完全な円になります。ですから、相関係数が0から1に向かって大きくなるほど、楕円は次第につぶれていくことになります。
なるほど、分ったような気がする。つまり、楕円の形は相関係数によって決まるんだ。
そうです。そこは良いですよね。
次に、さきほど"長さの話をしたいのか?"と言ってましたね。実は、きちんと計算して描いた楕円の周上では、降水量と傘の売上の平均つまり中心からの"距離"が同じということになります。
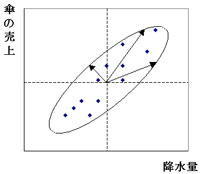
長さということは、当てずっぽうで言ったけど、この図の3本の矢印の長さが同じということになるのかい?
"長さ"ではありません。"距離"が同じになるのです。言い方を変えると、"仲間の程度"が同じということです。楕円上では全部仲間の程度が同じになります。その妥当性は、さきほど納得してくれましたよね。
しかし、長さと言ったら普通は距離のことだろう。仲間の程度と言うのならいいけど、距離と言われるとしっくり来ないなあ。
「二人の間の心の距離」とは言いますが、「心の長さ」とは言いませんよね。心の長さなんて言ってしまうと、全然雰囲気が出ません。

なるほど。まあ、意味するところはだいたい分ったよ。
ここで言う"距離"というのが、"仲間の程度"を表すと理解してください。楕円上では"仲間の程度"すなわち"距離"が同じです。そうすると、いろいろな距離の楕円を描くことができます。
いろいろな距離?
はい。距離なんですから、近い距離もあれば遠い距離もあります。今まで見てきた楕円は近い距離の楕円ということになります。仲間の程度が近いわけですから。
いくつか楕円を描いてみます。一番内側が距離1、その次が2、一番外側が3です。
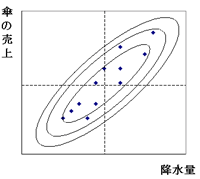
地図で見かける等高線みたいだな。
そうです。このことを立体的に説明すると、等高線と同じになります。
