MTシステム問答・応用編⑤
想像力が豊かですね。その通りのストーリーです。 では、どうやって定義するかです。 さきほどは円を描きましたが、今度は楕円を描いてみます。元の12個の点群をすっぽり囲む楕円を描くと、こんなふうになりますよね。
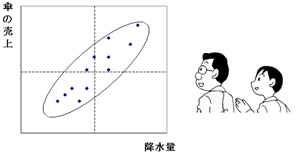
あ、ホントだ。言われてから気付いたけど、右上がりに細長く点がちらばっているんだから、楕円で囲むことができるね。
囲むだけなら四角でもひし形でも良いのかもしれませんが、やはり円の親戚である楕円で囲むのが一番自然でしょう。
こうして楕円を描いてみると、その内側であれば、どこに点を置いても元の12個の点群の"仲間"と言えそうですね。
そうすると、点Cは楕円の外にあって仲間とは言えない感じだ。楕円で囲むと感覚的にも納得できるね。
そうすると、こういう楕円をうまく描くことで、"普通の関係"の"仲間"と言えるかどうかが分るという訳かい?
その通りです。
では、この楕円をどういう理屈で描くのが良いかということになりますね。楕円ですから、細長いものや円に近いものまでいろいろとあります。

この傘の図では、わりとつぶれた楕円になっている。楕円のつぶれ方は何によって決まるんだろう?
先ほど、「相関係数」という言葉が出てきましたね。降水量と傘の売上の相関係数は0.9でした。相関係数は1以下ですから、0.9はかなり高いと言えます。
じゃあ、相関係数が0のときは楕円はどうなるの?
