MTシステム問答・応用編④
通常とは違う現象ねえ。雨が少ないのに傘が売れるというのはどんな場合だろう?
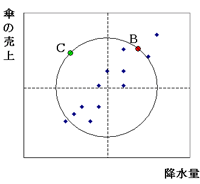
普通は考えにくいですよね。携帯電話付きの傘が発明されたとか。降水量とは別の売れる原因があったと考えるべきでしょう。それで、図の中に円を1個描いてみます。円の中心は、元の12個の点の平均の位置です。
円を描いた意味は何なの?
円は中心からの"長さ"が等しい点の集まりですね。定規で測ると、中心からの長さは皆同じです。実は、点BもCもこの円上にあるのです。
ああ、分った。長さの話をしようとしているね。さっきから"普通の関係"だとか、"仲間"だとか妙なことを言っていたよね。
かなり核心を突いています。もう、MTシステムを分っているんじゃないですか?
何を言ってるんだ。説明が始まったばかりじゃないか。
私が話している言葉の中に、普段と違う言葉というか、妙だなということを感じてくれていますよね・・・。それ自体がMTシステムの中心の考え方なのです・・・。いや、後で説明します。
話をまっすぐに続けましょう。 点BもCもこの円の上にありますね。ですから、中心から定規で測った長さは同じです。

うん、長さは同じだ。しかし、だ。BとCとでは"仲間と言えるかどうか"の程度が違う。つまり、仲間と言えるかどうかは定規で測った長さとは違う考えで定義しなければならない・・・。だいたい、こんなストーリーかな?
