MTシステム問答・応用編③
かんたんに言えば、関係とか関連のことですね。でも、ここでは数学の用語を使う必要があるので、相関とか相関係数という言葉を使わせてください。
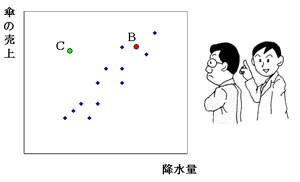
降水量と傘の売上はほぼ正の相関がありますね。横軸と縦軸の関係がきれいに直線の上に整列すると、相関係数は"1"ということになりますが、普通は多少ばらつくので1より小さくなります。この図の場合の相関係数は約0.9です。
相関はわかるけど、相関係数のことは忘れたなあ。
相関係数は、相関の強さを示す指標です。全く相関がなければ相関係数は"0"です。

ということは、降水量と傘の売上の相関係数が0.9ということは、かなり強い相関があるということになるんだね。
そうです。それで、このような関係が雨と傘の"普通の関係"ですよね。
次に、こうした"普通の関係"を前提として、ある月の降水量と傘の売上が点Bになり、別の月では点Cになったとします。
今、"普通の関係"と2回言ったね。何かたくらみがありそうだな・・・。
たくらみを感じますか。それを感じるということは、私の説明の予知と言うか、予測をしていることになりますね。
それで、点BとCとが普通の関係と比較したときに、その"普通の関係の仲間"と言えるかどうかを考えてみてください。
やっぱり何か企んでいる。"仲間と言えるかどうか"なんて、裏切り者かどうかを試しているみたいだ。
話がすぐにそれるな。ええと、点Bはほかの点の中に混じっているような印象だけど、点Cは孤立しているかな?
そうですね。点Bだと、降水量が多めで傘の売上もそれに見合って多くなっています。ところが、点Cは降水量が少ないのに、傘の売上がかなり多いことになります。通常とは違う何かの現象があったと考えた方が良さそうですね。
