MTシステム問答・応用編⑪

では、最後に文字パターンの距離をお見せします。整理の意味も含めて、順を追って説明します。
この"５"という文字は前に書いた16個の文字ですね。碁石は使っていませんが、意味は同じです。

これらの16個の文字から14種類の"変化の数"と"石の数"とを求めると以下の表が出来ます。この表は前にも見てもらいましたね。

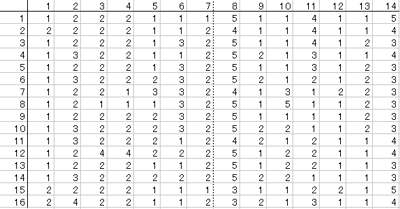
さらに全ての２組の列の相関係数を計算すると、さきほどびっくりした相関行列を求めることができます。

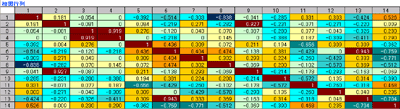
ここまでで準備は出来ました。数理手順としては"逆行列"という少し専門的な計算が行なわれますけど、それはコンピュータに任せるとして、下の４個の数字パターンのマハラノビス距離を計算してみます。これらは、先の16個のパターンには無いパターンです。

人間はパッとわかるんですがね。コンピュータにうまくわかるかどうかです。では計算してみましょう。マハラノビス距離は以下の通りとなります。

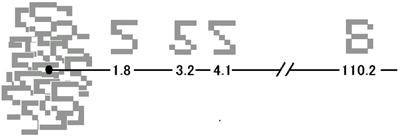
絵にして分り易いのは理科系も同じと思いますけどねえ。最近は理科系も文科系も関係ないことが多いんですけど。
それはそれとして、この図はまったく正しいです。こうすると、距離という概念がよくわかりますね。

ええ。わかってくると楽しいでしょう。
降水量と傘の売上の場合は、２次元で表せるので、距離が楕円のようにつぶれるという感覚が何となくは理解できましたよね。しかし、文字の場合は14次元ですね。相関のペアの数をちゃんと数えると、楕円が91個あることになります。91個の楕円を使って５という文字のパターンの距離を出した結果が、この図ということになります。

たった14個の変数でも、ペアの数は91個になります。何度も言いますが、考え方は一つで、定義通りの計算はコンピュータがやってくれます。
それで、あとはどこかに５と読めるかどうかの境界線を決めれば、パターン認識が完成します。一般論ですが、マハラノビス距離の境界線は、４あたりと言われています。つまり、４より小さければ元のデータ群の仲間と言えますし、それより大きければ仲間とは言いにくいということです。

その「かなりいい線」ということがパターン認識では重要なのです。パターン認識の良さを評価する方法にはいくつか方法がありますけど、人間が持つ"距離感"に近いことが一番大切なことです。人間の判断を置き換えるわけですから。

そう感じてもらえるとうれしいです。

では、その本を紹介しましょう。「入門MTシステム」 いう本です。詳しくは、このホームページの「テキスト」のボタンから見てください。