MTシステム問答・応用編⑩
行列についての、私の理解のプロセスがそうだったという話をしたかっただけです。 また話を戻して、特徴量・・・そうですね、一応数学らしく"変数"と言うことにしましょうか。ある状態を説明するためには、通常複数の変数を必要とします。それら変数の2個のペアずつの相関係数を求めて、全体のパターンの判定をしようというのが、マハラノビス博士の発見した方法です。
降水量と傘の事例は2次元、つまり変数が2個でした。そして、相関を考慮した"距離"が成立する、という話もしましたね。変数がたくさんあっても、変数間の相関に基づいた距離が計算できます。
ちょっと待って。あまりいっぺんに説明しないでくれ。フー。
えーと、相関係数ね。相関が大切。相関が崩れると顔も崩れる・・・、福笑いだね?
まあ・・・。あ、そうだ。相関以外にも大事なことを言うのを忘れてました。
相対位置が同じでも目や口の形が変わると表情が変わるということもあります。次の2枚の絵を見てください。

ん・・・? よく見ると、右の絵はあまり微笑んでいないような・・・。ああ、口が真一文字だ。
そうです。目や眉毛の形が変わると、これもまた表情が変わりますね。
相対位置が変わると顔つきが変わるという話をしましたが、口や目など、それぞれの形や大きさが変わると、やはり元の表情とは違うものになったり、別人になります。 降水量と傘の関係で言いますと、相関関係が正常のときと似ていると言っても、度を過ぎると仲間とは言えなくなることに相当します。次の図を見てください。
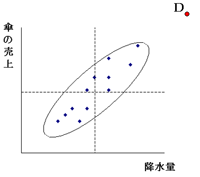
点Dは楕円のかなり外側にあるね。つまり距離が離れているということだ。度を過ぎるとというのは、降水量も傘の売上も例年より多いという意味かな?
そうです。距離という概念は、「普通の、あるいはいつも通りの関係に近いかどうか」が基本になりますが、それは相関関係が同じ傾向にあるかということと、もう一つ、程度もいつも通りか、ということの両方を含みます。
降水量の例では、点Dは降水量と傘の売上の相関関係という点では元のデータ群とほぼ同じなのですが、いずれも量がかなり増加しています。つまり元のデータ群からの距離は大きいことになります。
なるほど。その考えをモナリザに当てはめると、こんな絵になるかな。相対位置は変わらないけど、鼻を大きくしちゃった。ちょっと品が無くなるね。でも、この理解でいいんだろう?

うまい。
だいたい理解してもらえたようですので、そろそろまとめましょう。
パターンが同じかどうかは、変数の相関関係や値の大きさによって決まります。パターンの近さを計算する手段として、マハラノビス距離があります。どんなに変数が多くても、マハラノビス距離の計算ルールを用いると、妥当なパターンの距離を求めることができます。
マハラノビス距離は、基準となるデータ群からの距離を測る数理的手段です。
イメージはわかったけど、その"距離"なるものをまだ具体的に見ていないなあ。
